Prenons par exemple le système BINAIRE (BASE 2) qui ne dispose que de deux symboles : 0 et 1 (deux doigts!)
Compter par paquets : la base du système

On a tous eu un jour l’occasion de compter une quantité importante de petits objets :
des pièces de monnaie, des billes, des cartes,
Notre compte fini, on en effectue un deuxième afin d’être certain de ne pas s’être trompé.
Mais il est rare, malheureusement, de tomber deux fois sur le même résultat.
Et là, notre esprit ingénieux (!) nous conseille d’user d’un stratagème pour ne pas se faire posséder
une nouvelle fois par le grand nombre : on fait des petits paquets de 10 !
Et si cela ne suffit pas : avec 10 petits paquets de 10, nous formons un gros paquet de 100.
Nous réinventons le système de numération de
BASE 10 (système décimal)
Pourquoi « de base 10 », car pour obtenir un petit paquet, il faut 10 unités
et pour obtenir un gros paquet, il faut 10 petits paquets.
Pour passer au rang des dizaines (petits paquets), il faut 10 unités
et pour passer au rang des centaines (gros paquets), il faut 10 dizaines.
10 unités d'un rang valent 1 unité du rang immédiatement supérieur.
L'écriture décimale demande 10 symboles (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Nos 10 doigts en sont incontestablement à l’origine.
Que serait aujourd’hui notre système d’écriture si nous avions deux doigts seulement ?
Il est possible en effet d'écrire les nombres dans d'autres bases que la base décimale !
Prenons par exemple le système BINAIRE (BASE 2) qui ne dispose que de deux symboles : 0 et 1 (deux doigts!)

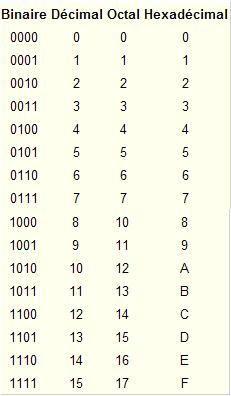
0 s’écrit 0 (en base 2)
1 s’écrit 1
2 s’écrit 10
3 s’écrit 11
4 s’écrit 100
5 s’écrit 101 etc…
Ce système est par exemple utilisé dans la programmation des ordinateurs.
En électronique, soit le circuit est fermé (0), soit il est ouvert (1).
A condition d’avoir un nombre suffisant de circuits, on peut coder n’importe quel nombre.
Le code ASCII utilise ainsi les nombres binaires pour représenter des symboles
tels les caractères, les chiffres, les signes de ponctuation...
Cette page est extraite de l'excellente Histoire des Nombres
www.col-camus-soufflenheim.ac-strasbourg.fr